Problem Definition

 

An important question in Finance is whether or not the stock market is efficient. The market is efficient if knowledge of past information or changes in a stock’s price tells us nothing about future changes in a stock’s price. In order to test market efficiency, the historical data of IBM’s daily stock return during 1994 is used. Then the data of the return on IBM during the last five days is used to predict tomorrow’s return. To see if the last five days can be used to predict today’s return, regression analysis is performed. If the market is efficient, the data from the last five days cannot be used to predict tomorrow’s return.

 

Data Collection

 

First, we need to collect the data. The collection process is done in a simple way in that it can be downloaded from any financial source website, such as Yahoo. Second, the return can be simply calculated using the formula (Pt/Pt-1) - 1. Click here to get the data file.

 

Model Formulation

 

Let’s see if daily price changes in IBM during 1994 are consistent with efficient markets. We want to determine if knowing that IBM went up yesterday or down yesterday would help us determine whether IBM will go up or down today. We would like to know the fraction of the time IBM goes up today after going down yesterday and the fraction of the time IBM goes up today after going up yesterday. The following is the example of the input data:

 

 

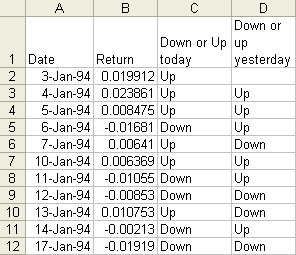
The data is analyzed using PivotTable. A PivotTable report is an interactive worksheet table that quickly combines and compares large amounts of data. Basically, it summarizes large amount of data using calculation methods you choose. You can rotate its rows and columns to see different summaries of the source data, and you can display the details for areas of interest. After sorting out the table, it should look as follow:

The figure above makes it clear that how IBM did yesterday has little effect on how it does tomorrow. If IBM went down yesterday it has a 53% chance of going down today, while if IBM went up yesterday it has a 55% chance of going up today. Since 53% and 55% are close, what happened yesterday appears to have little effect on what will happen today. This is consistent with the efficient market hypothesis of finance.

Time-series forecasting

Time-series forecasting is a collection of methods used to predict future outcomes based upon historical values. Time series analysis is an integral part of financial analysis that is interesting and useful, with applications to the prediction of interest rates, foreign currency risk, stock market volatility, and the like. In this project, we use regression to look for market efficiency. Regression is used to estimate the value of one variable when other variables are known.

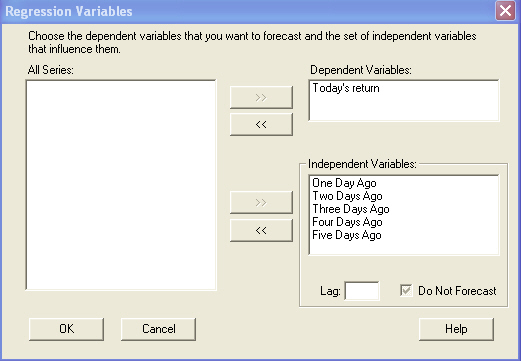
The next step is to use regression to look for market inefficiencies. First, the independent variables must be identified. The dependent variable is today’s return and the independent variables are the last five days of IBM returns. The input data should look as follow:

 

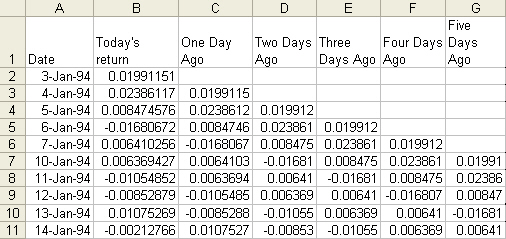
We are now ready to use CB Predictor to run the regression analysis. CB Predictor is just another time-series forecasting tool for Excel. It is a fully integrated Excel function that uses goodness of fit measures (RMSE, MAD or MAPE) and ranks the fits from best to worst. First, it will individually forecast the independent variables (in this case, the last five days returns) and then forecast the dependent variable (today’s return) using multiple regression.

 

 

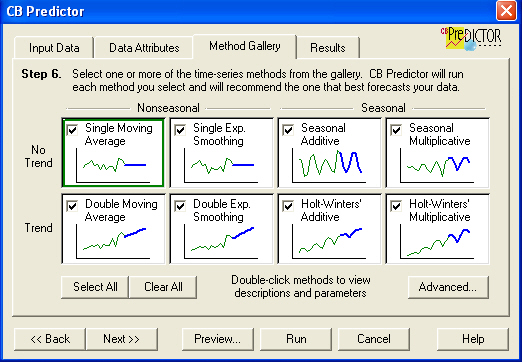
CB Predictor lets us forecasts multiple series of historical data at once using any of eight time-series forecasting methods shown below, including additional seasonal methods. We can forecast all the series, trying all the methods for each one. It will then tell us which method works best for each, according to one of the three error measures (RMSE, MAD, and MAPE).

 

 

 

 

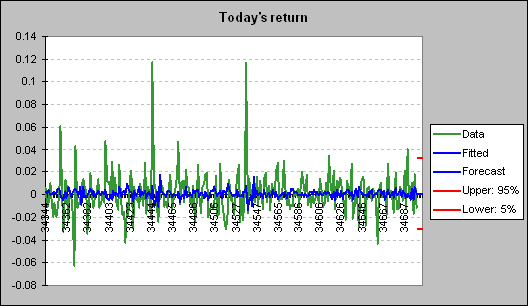
Summary:

 

 

 

 

 

 

Number of series: 6

 

 

 

 

 

 

Periods to forecast: 4

 

 

 

 

 

 

Seasonality: none

 

 

 

 

 

 

Error Measure: RMSE

 

 

 

 

 

 

Series: Today's return

 

 

 

 

 

 

 

 

 

 

 

 

Method: Multiple Linear Regression

 

 

 

 

 

 

 

 

 

 

 

Statistics:

 

 

 

 

 

 

R-squared: 0.038

 

 

 

 

 

Adjusted R-squared: 0.01799

 

 

 

 

 

SSE: 0.08575

 

 

 

 

 

 

F Statistic: 1.9016

 

 

 

 

 

F Probability: 0.09474

 

 

 

 

 

Durbin-Watson: 2.001

 

 

 

 

 

No. of Values: 247

 

 

 

 

 

Independent variables: 5 included out of 5 selected

 

 

 

 

 

 

 

 

Series Statistics:

 

 

 

 

 

 

Mean: 0.001142479

 

 

 

 

 

Std. Dev.: 0.019035226

 

 

 

 

 

Minimum: -0.06278027

 

 

 

 

 

Maximum: 0.1172249

 

 

 

 

 

Ljung-Box: 138.1209

 

 

 

 

 

 

 

 

 

 

 

Forecast:

 

 

 

 

 

 

 

 

 

 

 

 

 

Date

Lower: 5%

 

Forecast

Upper: 95%

 

 

12/31/1994

-0.029841488

 

0.001314582

0.032470651

 

 

1/2/1995

-0.02996433

 

0.001318907

0.032602144

 

 

1/3/1995

-0.030088215

 

0.001323232

0.03273468

 

 

1/5/1995

-0.030213154

 

0.001327558

0.03286827

 

 

Regression Variables:

 

 

 

 

 

 

 

 

 

 

 

 

Variable

 

 

Coefficient

t Statistic

Probability

 

Constant

 

 

0.001281

1.053

0.2934

 

One Day Ago

 

 

-0.09217

-1.4401

0.1511

 

Two Days Ago

 

 

-0.0767

-1.1976

0.2322

 

Three Days Ago

 

 

0.005791

0.09007

0.9283

 

Four Days Ago

 

 

-0.08692

-1.3604

0.175

 

Five Days Ago

 

 

0.1193

1.8705

0.06262

 

Interpretation:

 

The R square value of 0.038 means that the last five days of return explains only approximately 4% of the variation in today’s returns.

 

The equation for forecasting today’s IBM return would be:

 

Today’s return = .01281 –.09217(1 day ago) -.0767(2 days ago) + .005791(3 days ago) -.08692(4 days ago) + .1193(5 days ago)

 

Predicted results:

 

 

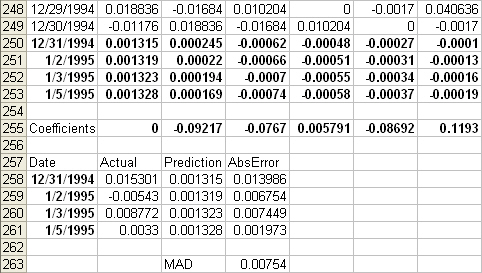
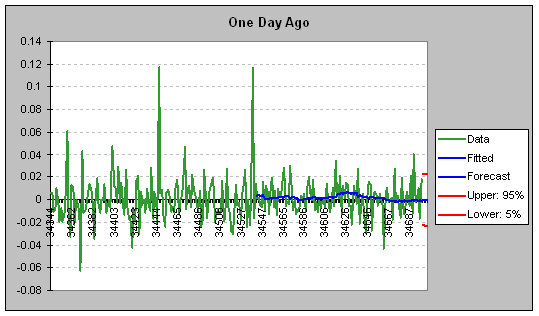
The number of periods predicted = 4 (December 31, 1994 – January 5, 1995). The model tells us that the predicted return for IBM stock on December 31, 1994 corresponds to the value of 0.001315, which deviates from the actual value of 0.015301, resulting in absolute error of 0.013986. We find that the MAD (Mean of Absolute Deviations) for these 4 data points to be 0.00754.

 

CB Predictor is useful in that it also forecasts each of the independent variables. The result of the forecasted first independent variable (one day ago) or first series is shown below:

 

Series: One Day Ago

 

 

 

 

 

 

 

 

 

 

 

 

Method: Double Moving Average

 

 

 

 

Parameters:

 

 

 

 

 

 

Periods:  69

 

 

 

 

 

Error: 0.01362

 

 

 

 

 

 

 

 

 

 

 

 

Series Statistics:

 

 

 

 

 

 

Mean: 0.001216062

 

 

 

 

 

Std. Dev.: 0.019020251

 

 

 

 

 

Minimum: -0.06278027

 

 

 

 

 

Maximum: 0.1172249

 

 

 

 

 

Ljung-Box: 138.7442

 

 

 

 

 

 

 

 

 

 

 

Forecast:

 

 

 

 

 

 

 

 

 

 

 

 

 

Date

Lower: 5%

 

Forecast

Upper: 95%

 

 

12/31/1994

-0.022246491

 

0.000245203

0.022736897

 

 

1/2/1995

-0.022363808

 

0.000219689

0.022803185

 

 

1/3/1995

-0.022481878

 

0.000194174

0.022870226

 

 

1/5/1995

-0.02260071

 

0.00016866

0.022938029

 

 

 

Suppose on December 30, 1994, IBM closing stock price is $100 and we had bought a share of IBM and decided to hold it. The model predicts that the returns for the next 4 days are 0.001315, 0.001319, 0.001323, and 0.001328 respectively. If the model is correct, the expected profit from buy and hold equals $0.529473 compared to the actual value of $2.2022. What we see is that the actual price does not behave according to what the model says. This tells us that historical information does not tell us anything about the future prices. This is consistent with efficient market hypothesis because prices already incorporate and reflect all relevant information. Hence, technical analysis, especially this simple regression technique we just performed, is of no use in predicting future market prices. In addition to that, the R-square regression value of 0.038 tells us that the last five days of return explains only approximately 4% of the variation in today’s returns.

 

 

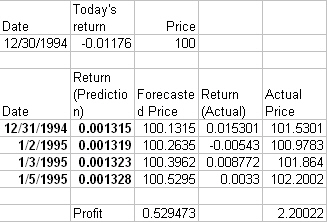
In conclusion, time-series analysis is vital in every aspect of business as it has its interesting and useful applications in such disparate fields as marketing, finance, and organizational behavior. It is important to be mindful that, despite the importance of the model, it is in fact only a representation of reality and not the reality itself. Accordingly, the model must adapt to reality; it is futile to attempt to adapt reality to the model.