Using Black-Scholes Option Formula to Find the Put Price
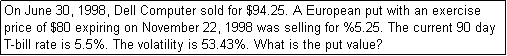
Text Box: On June 30, 1998, Dell Computer sold for $94.25. A European put with an exercise price of $80 expiring on November 22, 1998 was selling for %5.25. The current 90 day T-bill rate is 5.5%. The volatility is 53.43%. What is the put value?
Input data
Stock price (S) $94.25 today 6/30/1998 35976
DATEVALUE("6/30/98")
Exercise price (X) $80 expire 11/22/1998 36121
DATEVALUE("11/22/98")
Duration (t) 0.39726 difference 145.00
Interest rate (r) 5.35%
Text Box: Risk-free rate (rf) input to the Black-Scholes formula is the continuously compounded rate. Ln (1 + current 90 day T-Bill Rate)
Implied volatility (s) 53.43%
d1 0.71833 N(d1) 0.763723
d2 0.381589 N(d2) 0.648617
Call price (C) $21.18
Put price (P) $5.25
Xe-rt N(-d2) - SN(-d1)
C = N(d1)S - e-rT XN(d2 )
Text Box: N(z) is the probability that a random draw from a standard normal distribution is less than z. Think of N(z) as a probability (it is!). Roughly, it is the probability that the option expires in-the-money