Prepared by: Vinchel Budihardjo & Truong D.Vu

 

Use of Monte Carlo Simulation

 

The usefulness of financial statement projections for corporate financial management is undisputed. Such projections, called pro forma financial statements, are the bread and butter of much corporate financial analysis. Pro forma financial statements look at the links between the balance sheets and income statements and more importantly the flow of funds in the future. A pro forma income statement is similar to a historical income statement, except it projects the future rather than tracks the past. It the projection predicts a downturn in profitability, you can make operational changes such as increasing prices or decreasing costs before these projections become reality. A company’s future profitability, borrowing and many other quantities are all highly uncertain quantities. It seems natural to run a simulation to obtain a range of values on future profitability and borrowing. Simulation is related to both scenario and sensitivity analysis. It ties together sensitivities and input variable probability distributions. We can play the usual “what-if” games of simulation models, and we can ask what strains on the firm may be caused by changes in certain variables such as sales and expenses. The purpose of this exercise is to illustrate the use of Monte Carlo Simulation to form the basis for valuation and credit analysis. First of all, we need to get the historical financial statements data for Home Depot and then we create a simulation.

 

Relevant Data

 

Figure 1 below shows the relevant data for Home Depot in 1995. All numbers are in millions of dollars. Note that Sources = Uses and Assets = Liabilities + Equities. Given the actual financial statements for Home Depot, we can forecast their financial statement for the next year (1996). Next year revenue (t+1) is simply the value of t (current year) multiplied by a constant value shown in column D. This is the trick in linking year t with the next year (t+1). To see the key relationships, click here to get the spreadsheet. Since, the spreadsheet is an @Risk spreadsheet, you also need to get .rsk file. After running the simulation, both Excel (XLS) and @Risk (RSK) files need to be saved separately. If the associated .rsk file is not saved, then reopening an Excel file necessitates rerunning the simulation to obtain the results.

 

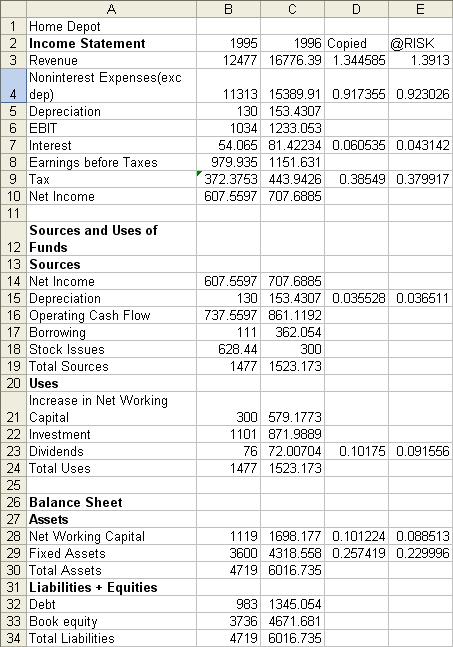
Figure 1

 

The Dynamics of the Model

 

In a simulation analysis, the computer begins by picking at random a value for each of the uncertain variables (Revenue Growth, percentage of Non-interest expenses to Revenue, Interest rate on Long-Term debt, Tax rate, Depreciation on Fixed-Assets, Dividend payout rate, Net WC and Fixed Assets) based on its specified probability distribution. We assign the following names to these variables: a1-a8. Monte Carlo variables assume that the processes being studied are independent of each other and that each value is a random draw from a distribution, or serially independent. The end result of Monte Carlo simulation is the continuous probability distribution with its own expected value and standard deviation. A simulation is more comprehensive than scenario analysis because it considers an infinite number of possible outcomes. The solution strategy in this exercise involves the use of historical financial statements analysis to determine which income statement and balance sheet items are close to being a constant percentage of sales. To apply the forecast, we use the data from year 1990 to 1995 and calculate the average and standard deviation of each item. Note that the parameters a1-a8 drive the model. Figure 2 shows the work in estimating the mean and standard deviation of these parameters.

 

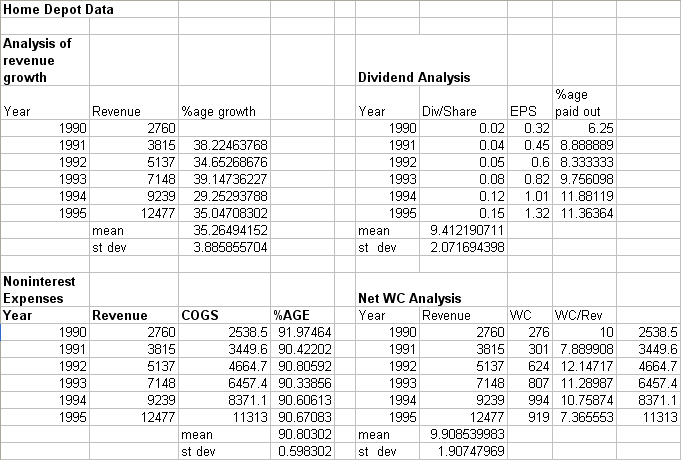
Figure 2

 

The mean or average value is used as a measure of expected value and the standard deviation (or coefficient of variation) is used as a measure of risk. The assumption here is that each of the eight items can be represented by a continuous random distribution. We make them =RISKNormal functions to model the fact that each constant may differ in different years. This drives the randomness of the model. As an example consider a1 (Revenue Growth). This parameter measure the year to year growth in revenue. For 1991-1995, we found the average growth in revenue to be 35.26% and the standard deviation to be 3.89%. To model the simulation, we use the formula RiskNormal (1.3526, 0.0388). The formula for a2 = RiskNormal (0.0991, 0.0191).

 

Here’s the list of inputs with the formulas assigned:

 

 

If you look at the Financial Statement data, you will notice that net income influences borrowing, borrowing influences debt, debt influences interest, and interest influences income. In Excel, this is referred to as circular reference. There is a way of resolving the circular reference problem. Simply go to “Tools”, then choose “Options” “Calculation” “Automatic” and check “Iterations” and put in 1000 for maximum iterations. You will see that Assets = Liabilities + Equities and Uses = Sources.

 

Before running the simulation, we will create a macro that will paste the constant value (as numbers, not formulas) from the simulation (column E) to column D. Then it will feed into column C and it will resolve the circularities. The macro name used is Macro2. Under @Risk simulation setting, we ask @Risk to run Macro2 before each iteration of a simulation. The sequence of events would be:

 

  1. Run Macro2
  2. Compute @Risk functions and calculate output cells
  3. Run Macro2, etc

 

 

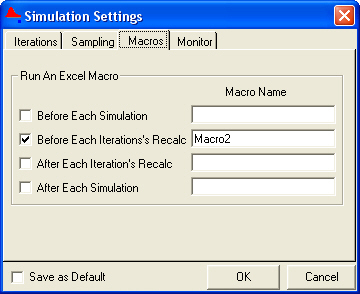
This ensures that before each time the value of an output cell is tabulated, new values of a1-a8 will be generated.

 

We’re now ready to run the simulation. The only output we are trying to measure is the Net Income. After 1000 iterations, @Risk produces the following results:

 

Summary Statistics

Statistic

Value

%tile

Value

Minimum

505.4887695

5%

674.0304565

Maximum

1102.032837

10%

705.9438477

Mean

811.5698513

15%

725.0234375

Std Dev

85.46608282

20%

743.0560913

Variance

7304.451313

25%

755.5171509

Skewness

0.039828427

30%

766.8305664

Kurtosis

3.216118724

35%

779.039856

Median

810.1477051

40%

790.0019531

Mode

818.5773621

45%

801.8696289

Left X

674.0304565

50%

810.1477051

Left P

5%

55%

819.0309448

Right X

952.2886963

60%

828.7329102

Right P

95%

65%

840.2873535

Diff X

278.2582397

70%

848.4483643

Diff P

90%

75%

865.7454224

#Errors

0

80%

882.7453613

Filter Min

 

85%

900.5479736

Filter Max

 

90%

923.5115967

#Filtered

0

95%

952.2886963

 

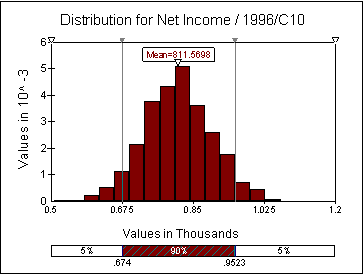
A picture is worth a thousand words and the summary statistics above shows the probability distribution of the outcome. We see that on average, we expect Home Depot’s 1996 Net Income to be 811 million. They actually made 733 million (according to the actual data), which was in between the 15th and 20th percentile of what we expected.

 

 

@Risk is such a powerful tool in that it gives you countless reporting and graphing options. To see the complete results, click here.

 

Conclusion

 

We can use this simulation technique to forecast as many years ahead as we like. This does not mean it goes with the expectation that past revenue growth assumptions hold. A company could have its business cycle and as such is on S-shaped curve of growth that most companies follow. Also, the industry is expected to become more competitive. This could affect some of the variables we used such as margin (as factored into a2). This model gives you flexibility to build in (with If statements) future assumptions about the industry and the firm behavior (for example: stock issuing policy). In the example above, the revenue growth follows a random normal variable. We could have instead used the other function that takes some of the values as equally likely scenarios of future growth. Let’s say, the revenue growth could be one of the following values: 1.3822, 1.2565, 1.3952, or 1.2585. Instead of using the =RISKNormal function, we could input the function: RISKDUniform({1.3822,1.2565,1.3952,1.2585}) as the formula.