Situation Description and Objective

 

This exercise is based on Example 4.2 (Worker and Production Planning at SureStep) in the textbook. Most companies need to determine a production schedule in order to meet the demand of their customers. We will use Excel Solver to plan a production schedule that will minimize total costs given certain constraints. During the next 4 months, SureStep Company wants to meet on time the following demands for pairs of shoes:

 

Month

Pairs of shoes

1

3000

2

5000

3

2000

4

1000

 

Note that this is the certainty assumption that the company faces. Normally, we do not know how much to produce in each month given the limited amount of resources needed to produce the shoes. But, here, for the sake of simplicity, we set the target to those 4 months values. The following are the input variables to begin with:

 

 

Figure 1

 

The solution requires that we keep track of each month’s beginning inventory, ending inventory, production and all costs

The goal of this spreadsheet is to determine the optimal production schedule and labor policy

 

We will look at some of the variables that will determine the final output.

 

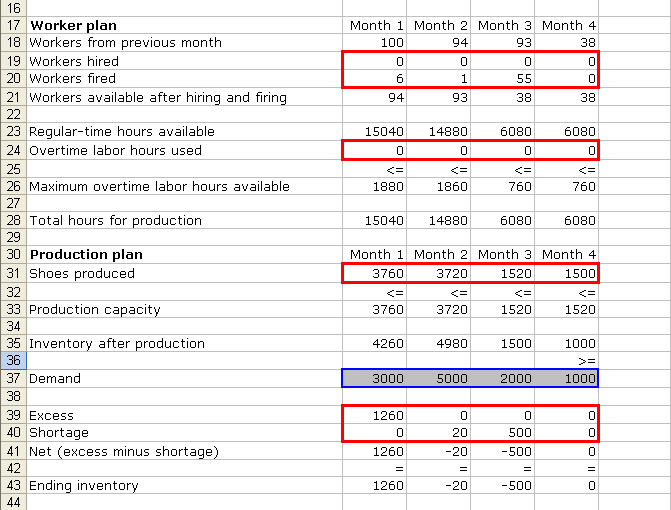
We know that the company has 100 workers at the beginning of month 1. If they decided to hire 0 worker and fire 6, then the number of workers available after firing and hiring = 94. The # of worker to hire and the # of workers to fire at the beginning of each month are the decision variables. Each worker has 160 hours per month. Hence, the “regular total hours available” = 94 x 160 = 15040 hours. This does not include the number of overtime labor hours the company decides to use. Now, we have 96 workers available to produce shoes. Each worker has overtime limit of 20 hours. The maximum overtime hours available = 96 x 20 = 1920. Does it mean that the company will use the maximum overtime hours available? The overtime labor hours used is the decision variable and it varies from month to month. Remember that the company wants to use the combination of variables that best maximize the total profit. Let’s say, the company uses 0 overtime hours. Total hours used for production = regular total hours available + overtime labor hours used (15040 = 15040 + 0)

 

Next, we determine the “production capacity” by dividing the “number of hours used for production” by the “number of hours used to produce a pair of shoes.” For example, if there is 15040 total hours for production and it takes 4 labor hours to produce a pair of shoes, then the production capacity = 15040/4 = 3760

 

We know that the production capacity in month 1 = 3760. Suppose the company decides to produce 3760 shoes (The decision to produce x number of shoes is the decision variable). Then “inventory after production” is simply the addition of last month’s ending inventory (500) to this month’s # of shoes produced (3760). The demand for the first month is 3000. Ending Inventory is calculated by subtracting “demand” by “Inventory after production.” If the result is negative, then it means the company fails to meet the desired demand. A shortage cost = $15 per unit. If “demand” is less than “inventory after production,” the company has some shoes left in the inventory that is not sold. The holding cost = $3 per pair of shoes. This example shows us that the company has 1260 ending inventory. The cost of holding excess inventory = 1260 x $3 = $3780.

 

The company wants to make sure that by the end of month 4, demand is met. This means that Ending Inventory in month 4 cannot be negative (the company will not incur shortage cost). If there’s excess inventory, the company will incur holding cost. If the ending inventory = 0, the company does not incur any cost. This is consistent with the idea of minimizing cost.

 

Figure 2

 

Click here to get the spreadsheet

 

Variables & Attributes

 

Variables

How Measured

Related to

# of workers available after hiring and firing

Integer

# of workers from previous month & hiring of new workers and firing of existing workers

Regular-time hours available

Hours

# of workers after hiring and firing & each worker’s hours per month before receiving overtime

Maximum overtime labor hours available

Hours

# of workers after hiring and firing & each worker’s 20 overtime hours per month

Total hours for production

Hours

Regular-time hours available & Overtime labor hours used

Production capacity

Number of pairs of shoes (cannot be fraction)

Total hours for production & # of labor hours required to produce a pair of shoes

Inventory after production

Number of pairs of shoes (cannot be fraction)

Prior month’s ending inventory & # of shoes produced in the current month

Ending inventory

Number of pairs of shoes (cannot be fraction)

Inventory after production & # of units demanded

 

 

Decision Variables

How Measured

Subject to constraints:

# of workers hired

Integer

Value has to be integer (can not be fraction)

# of workers fired

Integer

Value has to be integer (can not be fraction)

Overtime labor hours used

Hours

Maximum overtime labor hours available

Shoes produced

Number of pairs of shoes (cannot be fraction)

Production capacity

Excess shoes

Number of pairs of shoes (cannot be fraction)

 

Shortage shoes

Number of pairs of shoes (cannot be fraction)

 

 

Mathematical Model Formulation

 

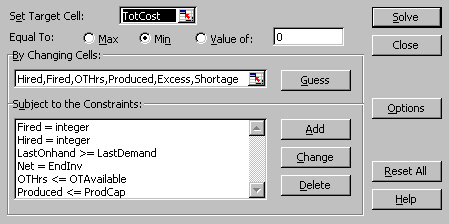
The objective of this linear model is to minimize total costs. Therefore, “total costs” has to be set as a target cell. We choose to minimize total costs by adjusting the number of workers hired (B19:E19), the number of workers fired (B20:E20), the overtime labor hours used (B24:E24) and the number of shoes to produce (B31:E31). These are the decision variables. The values in these changing cells can be changed to optimize the objective.

 

Figure 3

 

Constraints must be set as follows:

 

The number of workers hired & fired must be set as integer (cannot be fraction). The inventory after production in month 4 must be bigger or equal to the number of shoes demanded in that month. Overtime labor hours used in each month cannot exceed the maximum overtime labor hours available. The number of shoes produced in each month cannot exceed the full production capacity. Net excess minus shortage equals Ending Inventory. If there’s excess of 10 pairs of shoes, then there’s no shortage. If there’s excess of -10 pairs of shoes, then shortage = 10 pairs.

The values in the changing cells cannot be negative.

 

Development of Spreadsheet Model

 

We have already shown the steps to develop the spreadsheet model. The first step is to enter the values given in the exercise in the input cells (shown in Figure 1). Next, we input trial values in the changing cells. The formulas for other variables must also be set. For example, Production capacity in month 1 (B33) = Total hours for production (B28) x number of labor hours used to produce a pair of shoes (B12).

 

Then we invoke Excel Solver and set it up as shown in Figure 3 (subject to Constraints). Since this model is a linear model, we go to Options menu and check both “Assume Linear Model” and “Assume Non-Negative.”

 

We’re now ready to tell Solver to find the optimum solution. Clicking Solve button will do all the jobs in no time.

 

The final step is to run sensitivity analysis and see the impact of the increase/decrease in input variable on the output.

 

Results

 

We found that in order to minimize total costs, we will have to fire some workers in month 1-3 and hire none in each of the 4 months. Overtime labor hours will not be used. The company will have to use full production capacity. Finally, we see that the company will have to incur holding cost in month 1 and shortage cost in month 2 & 3. There is no shortage or holding cost in the last month because the company has to meet the demand. 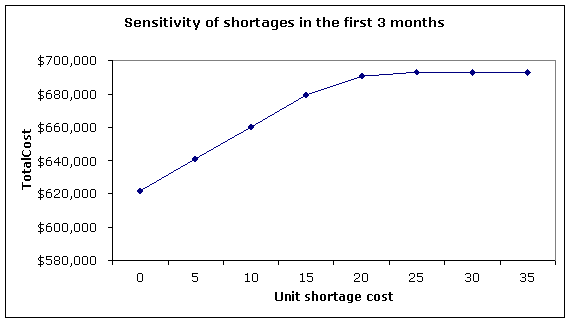The minimum total costs solver found is $690,180. Let’s do what-if analysis. Is there any way to decrease the total costs by changing any of the input variable? We will change the unit shortage cost (increment of $5) to determine if there is a better alternative for SureStep.

 

Sensitivity of shortages in the first three months and total cost to unit shortage cost

 

Unit shortage cost

Shortage1

Shortage2

Shortage3

TotalCost

 

$B$40

$C$40

$D$40

$F$53

$0

0

2,280

1,640

$621,740

$5

0

2,220

1,580

$640,920

$10

0

2,220

1,580

$659,920

$15

0

2,220

1,580

$678,920

$20

0

20

500

$690,180

$25

0

20

20

$692,780

$30

0

0

0

$692,820

$35

0

0

0

$692,820

 

As we see, when the unit shortage cost is below $20, SureStep is willing to incur large shortages – at significantly lower total cost. However, shortages become much less attractive when the unit shortage cost increases, and no shortages are incurred at all when this unit cost is above $25.

 

 

 

DSS Guidelines & Limitation

 

This model proves to be simple but useful in assisting labor and production planning. It is essentially every manufacturing company’s problem. The model could be enhanced by including other variables which may prove to be relevant in addressing company’s issues. All in all, this spreadsheet model is a linear model that helps solve the optimal value of an output given certain constraints and formulas that follow it. We have proven that we can use Excel Solver to solve an interesting optimization problem such as this one. We know that the target cell in this model is a linear function of the changing cells. The left-hand and right-hand sides of each constraint are linear functions of the changing cells. When we use the functions =IF, =ABS, =MAX, =MIN which depends on any of the models changing cells, then the model becomes nonlinear. This in turn become an optimization problem for which Excel Solver is ill suited to find optimal solutions. Fortunately, genetic algorithm technique, as discussed in the textbook, can be used as a superior tool to find the optimal solution. The problem becomes more challenging if there’s uncertainty factor in it, such as a demand which is normally distributed with certain monthly mean and standard deviation.